| Titel | Inhalt | Suchen | Index | DOC | Handbuch der Java-Programmierung, 7. Auflage |
| << | < | > | >> | API | Kapitel 50 - Sicherheit und Kryptografie |
Thema dieses Kapitels ist es, die in Java verfügbaren Sicherheitsmechanismen vorzustellen. Wir werden dabei zunächst auf allgemeine Konzepte aus dem Gebiet der Kryptografie und ihre Implementierung in Java eingehen. Anschließend werden die eingebauten Sicherheitsmechanismen von Java vorgestellt. Zum Abschluss zeigen wir, wie signierte Applets erstellt und verwendet werden und wie mit ihrer Hilfe eine fein differenzierte Sicherheitspolitik etabliert werden kann. Zunächst sollen allerdings wichtige Begriffe erläutert werden, die für das Verständnis der nachfolgenden Abschnitte von Bedeutung sind.
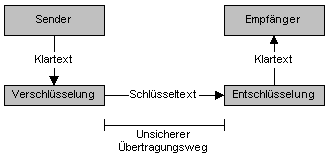
Angenommen, ein Sender will eine Nachricht an einen Empfänger übermitteln. Soll das geschehen, ohne dass ein Dritter, dem die Nachricht in die Hände fallen könnte, diese entziffern kann, könnte sie verschlüsselt werden. Der ursprüngliche Nachrichtentext (der als Klartext bezeichnet wird) wird dabei mit Hilfe eines dem Sender bekannten Verfahrens unkenntlich gemacht. Das als Schlüsseltext bezeichnete Ergebnis wird an den Empfänger übermittelt und mit Hilfe eines ihm bekannten Verfahrens wieder in den Klartext zurückverwandelt (was als Entschlüsseln bezeichnet wird).
Abbildung 50.1: Verschlüsseln einer Nachricht
Solange der Algorithmus zum Entschlüsseln geheim bleibt, ist die Nachricht sicher. Selbst wenn sie auf dem Übertragungsweg entdeckt wird, kann kein Dritter sie entschlüsseln. Wird das Entschlüsselungsverfahren dagegen entdeckt, kann die Nachricht (und mit ihr alle anderen Nachrichten, die mit demselben Verfahren verschlüsselt wurden) entziffert werden.
Um den Schaden durch das Entdecken eines Verschlüsselungsverfahrens gering zu halten, werden die Verschlüsselungsalgorithmen in aller Regel parametrisiert. Dazu wird beim Verschlüsseln eine als Schlüssel bezeichnete Ziffern- oder Zeichenfolge angegeben, mit der die Nachricht verschlüsselt wird. Der Empfänger benötigt dann zusätzlich zur Kenntnis des Verfahrens noch den vom Sender verwendeten Schlüssel, um die Nachricht entziffern zu können.
Die Wissenschaft, die sich mit dem Verschlüsseln und Entschlüsseln von Nachrichten und eng verwandten Themen beschäftigt, wird als Kryptografie bezeichnet. Liegt der Schwerpunkt mehr auf dem Entschlüsseln, (insbesondere dem Entziffern geheimer Botschaften), wird dies als Kryptoanalyse bezeichnet. Die Kryptologie schließlich bezeichnet den Zweig der Mathematik, der sich mit den formal-mathematischen Aspekten der Kryptografie und Kryptoanalyse beschäftigt.
Seit dem Altertum sind einfache Verschlüsselungsverfahren bekannt. Zu ihnen zählen beispielsweise die Substitutions-Verschlüsselungen, bei denen einzelne Buchstaben systematisch durch andere ersetzt werden. Angenommen, Klartexte bestehen nur aus den Buchstaben A bis Z, so könnte man sie dadurch verschlüsseln, dass jeder Buchstabe des Klartextes durch den Buchstaben ersetzt wird, der im Alphabet um eine feste Anzahl Zeichen verschoben ist. Als Schlüssel k kann beispielsweise die Länge der Verschiebung verwendet werden. Ist k beispielsweise 3, so würde jedes A durch ein D, jedes B durch ein E, jedes W durch ein Z, jedes X durch ein A usw. ersetzt werden.
Dieses einfache Verfahren wurde beispielweise bereits von Julius Cäsar verwendet, um seinen Generälen geheime Nachrichten zu übermitteln. Es wird daher auch als Cäsarische Verschlüsselung bezeichnet. Das folgende Listing zeigt eine einfache Implementierung dieses Verfahrens, bei dem Schlüssel und Klartext als Argument übergeben werden müssen:
001 /* Listing5001.java */
002
003 public class Listing5001
004 {
005 public static void main(String[] args)
006 {
007 int key = Integer.parseInt(args[0]);
008 String msg = args[1];
009 for (int i = 0; i < msg.length(); ++i) {
010 int c = (msg.charAt(i) - 'A' + key) % 26 + 'A';
011 System.out.print((char)c);
012 }
013 }
014 }
|
Listing5001.java |
Um die Nachricht zu entschlüsseln, verwendet der Empfänger
dasselbe Verfahren, allerdings mit dem Schlüssel 26 - k:
--->java Test2 3 HALLO
KDOOR
--->java Test2 23 KDOOR
HALLO
Ein ähnlich weitverbreitetes Verfahren besteht darin, jedes Zeichen des Klartexts mit Hilfe des Exklusiv-ODER-Operators mit dem Schlüssel zu verknüpfen. Durch dessen Anwendung werden alle Bits invertiert, die zu einem gesetztem Bit im Schlüssel korrespondieren, alle anderen bleiben unverändert. Das Entschlüsseln erfolgt durch erneute Anwendung des Verfahrens mit demselben Schlüssel.
 |
Ein Verfahren, bei dem Ver- und Entschlüsselung mit demselben Algorithmus und Schlüssel durchgeführt werden, wird als symmetrische Verschlüsselung bezeichnet. |
|
 |
Eine einfache Implementierung der Exklusiv-ODER-Verschlüsselung zeigt folgendes Listing:
001 /* Listing5002.java */
002
003 public class Listing5002
004 {
005 public static void main(String[] args)
006 {
007 int key = Integer.parseInt(args[0]);
008 String msg = args[1];
009 for (int i = 0; i < msg.length(); ++i) {
010 System.out.print((char)(msg.charAt(i) ^ key));
011 }
012 }
013 }
|
Listing5002.java |
Ein Anwendungsbeispiel könnte so aussehen:
--->java Test2 65 hallo
) --.
--->java Test2 65 ") --."
hallo
 |
 |
Dass die Rückkonvertierung über die Kommandozeile hier geklappt hat, liegt daran, dass die Verschlüsselung keine nichtdarstellbaren Sonderzeichen produziert hat (der Schlüssel 65 kippt lediglich 2 Bits in jedem Zeichen). Im Allgemeinen sollte der zu ver- oder entschlüsselnde Text aus einer Datei gelesen und das Resultat auch wieder in eine solche geschrieben werden. Dann können alle 256 möglichen Bitkombinationen je Byte zuverlässig gespeichert und übertragen werden. |
|
 |
Derart einfache Verschlüsselungen wie die hier vorgestellten sind zwar weit verbreitet, denn sie sind einfach zu implementieren. Leider bieten sie aber nicht die geringste Sicherheit gegen ernsthafte Krypto-Attacken. Einige der in letzter Zeit bekannt gewordenen (und für die betroffenen Unternehmen meist peinlichen, wenn nicht gar kostspieligen) Fälle von Einbrüchen in Softwaresysteme waren darauf zurückzuführen, dass zu einfache Sicherheitssysteme verwendet wurden.
Wir wollen diesen einfachen Verfahren nun den Rücken zuwenden, denn seit dem JDK 1.2 gibt es in Java Möglichkeiten, professionelle Sicherheitskonzepte zu verwenden. Es ist ein großer Vorteil der Sprache, dass auf verschiedenen Ebenen Sicherheitsmechanismen fest eingebaut wurden und eine missbräuchliche Anwendung der Sprache erschwert wird. In den folgenden Abschnitten werden wir die wichtigsten dieser Konzepte vorstellen.
Ein Message Digest ist eine Funktion, die zu einer gegebenen Nachricht eine Prüfziffer berechnet. Im Gegensatz zu ähnlichen Verfahren, die keine kryptografische Anwendung haben (siehe z.B. hashCode in Abschnitt 9.1.2), muss ein Message Digest zusätzlich folgende Eigenschaften besitzen:
Ein Message Digest wird daher auch als Einweg-Hashfunktion bezeichnet. Er ist meist 16 oder 20 Byte lang und kann als eine Art komplizierte mathematische Zusammenfassung der Nachricht angesehen werden. Message Digests haben Anwendungen im Bereich digitaler Unterschriften und bei der Authentifizierung. Allgemein gesprochen werden sie dazu verwendet, sicherzustellen, dass eine Nachricht nicht verändert wurde. Bevor wir auf diese Anwendungen in den nächsten Abschnitten zurückkommen, wollen wir uns ihre Implementierung im JDK 1.2 ansehen.
Praktisch alle wichtigen Sicherheitsfunktionen sind im Paket java.security oder einem seiner Unterpakete untergebracht. Ein Message Digest wird durch die Klasse MessageDigest implementiert. Deren Objekte werden nicht direkt instanziert, sondern mit der Methode getInstance erstellt:
public static MessageDigest getInstance(String algorithm) throws NoSuchAlgorithmException |
java.security.MessageDigest |
Als Argument wird dabei die Bezeichnung des gewünschten Algorithmus angegeben. Im JDK 1.2 sind beispielsweise folgende Angaben möglich:
Nachdem ein MessageDigest-Objekt erzeugt wurde, bekommt es die Daten, zu denen die Prüfziffer berechnet werden soll, in einzelnen Bytes oder Byte-Arrays durch fortgesetzten Aufruf der Methode update übergeben:
public void update(byte input) public void update(byte[] input) public void update(byte[] input, int offset, int len) |
java.security.MessageDigest |
Wurden alle Daten übergeben, kann durch Aufruf von digest das Ergebnis ermittelt werden:
public byte[] digest() |
java.security.MessageDigest |
Zurückgegeben wird ein Array von 16 bzw. 20 Byte (im Falle anderer Algorithmen möglicherweise auch andere Längen), in dem der Message Digest untergebracht ist. Ein Aufruf führt zudem dazu, dass der Message Digest zurückgesetzt, also auf den Anfangszustand initialisiert, wird.
Das folgende Listing zeigt, wie ein Message Digest zu einer beliebigen Datei erstellt wird. Sowohl Algorithmus als auch Dateiname werden als Kommandozeilenargumente übergeben:
001 /* Listing5003.java */
002
003 import java.io.*;
004 import java.security.*;
005
006 public class Listing5003
007 {
008 /**
009 * Konvertiert ein Byte in einen Hex-String.
010 */
011 public static String toHexString(byte b)
012 {
013 int value = (b & 0x7F) + (b < 0 ? 128 : 0);
014 String ret = (value < 16 ? "0" : "");
015 ret += Integer.toHexString(value).toUpperCase();
016 return ret;
017 }
018
019 public static void main(String[] args)
020 {
021 if (args.length < 2) {
022 System.out.println(
023 "Usage: java Listing5003 md-algorithm filename"
024 );
025 System.exit(0);
026 }
027 try {
028 //MessageDigest erstellen
029 MessageDigest md = MessageDigest.getInstance(args[0]);
030 FileInputStream in = new FileInputStream(args[1]);
031 int len;
032 byte[] data = new byte[1024];
033 while ((len = in.read(data)) > 0) {
034 //MessageDigest updaten
035 md.update(data, 0, len);
036 }
037 in.close();
038 //MessageDigest berechnen und ausgeben
039 byte[] result = md.digest();
040 for (int i = 0; i < result.length; ++i) {
041 System.out.print(toHexString(result[i]) + " ");
042 }
043 System.out.println();
044 } catch (Exception e) {
045 System.err.println(e.toString());
046 System.exit(1);
047 }
048 }
049 }
|
Listing5003.java |
 |
Im Paket java.security gibt es zwei Klassen, die einen Message Digest mit einem Stream kombinieren. DigestInputStream ist ein Eingabe-Stream, der beim Lesen von Bytes parallel deren Message Digest berechnet; DigestOutputStream führt diese Funktion beim Schreiben aus. Beide übertragen die eigentlichen Bytes unverändert und können dazu verwendet werden, in einer Komposition von Streams »nebenbei« einen Message Digest zu berechnen. |
|
 |
Ein wichtiges Anwendungsgebiet von Message Digests ist die Authentifizierung, d.h. die Überprüfung, ob die Person oder Maschine, mit der kommuniziert werden soll, tatsächlich »echt« ist (also die ist, die sie vorgibt zu sein). Eine Variante, bei der ein Anwender sich mit einem Benutzernamen und Passwort autorisiert, kann mit Hilfe eines Message Digest in folgender Weise realisiert werden:
Bemerkenswert daran ist, dass das System nicht die Passwörter selbst speichert, auch nicht in verschlüsselter Form. Ein Angriff auf die Benutzerdatenbank mit dem Versuch, gespeicherte Passwörter zu entschlüsseln, ist daher nicht möglich. Eine bekannte (und leider schon oft erfolgreich praktizierte) Methode des Angriffs besteht allerdings darin, Message Digests zu allen Einträgen in großen Wörterbüchern berechnen zu lassen, und sie mit den Einträgen der Benutzerdatenbank zu vergleichen. Das ist einer der Gründe dafür, weshalb als Passwörter niemals Allerweltsnamen oder einfache, in Wörterbüchern verzeichnete, Begriffe verwendet werden sollten.
Eine weitere Anwendung von Message Digests besteht darin, die Existenz von Geheimnissen oder den Nachweis der Kenntnis bestimmter Sachverhalte nachzuweisen, ohne deren Inhalt preiszugeben - selbst eigentlich vertrauenswürdigen Personen nicht. Dies wird in Bruce Schneiers Buch als Zero-Knowledge Proof bezeichnet und funktioniert so:
Das Geheimnis ist nicht veröffentlicht, der Nachweis für seine Existenz zum Zeitpunkt X aber erbracht. Muss A Jahre später die Existenz dieser Informationen nachweisen, holt es die Diskette mit dem Geheimnis aus dem Tresor, berechnet den Message Digest erneut und zeigt dessen Übereinstimmung mit dem seinerzeit in der Zeitung veröffentlichten.
Eine weitere Anwendung von Message Digests besteht im Erstellen von Fingerprints (also digitalen Fingerabdrücken) zu öffentlichen Schlüsseln (was das genau ist, wird in Abschnitt 50.1.5 erklärt). Um die Korrektheit eines öffentlichen Schlüssels nachzuweisen, wird daraus ein Message Digest berechnet und als digitaler Fingerabdruck an prominenter Stelle veröffentlicht (beispielsweise in den Signaturen der E-Mails des Schlüsselinhabers).
Soll vor der Verwendung eines öffentlichen Schlüssels überprüft werden, ob dieser auch wirklich dem gewünschten Inhaber gehört, ist lediglich der (durch das Schlüsselverwaltungsprogramm ad-hoc berechnete) Fingerprint des öffentlichen Schlüssels mit dem in der E-Mail veröffentlichten zu vergleichen. Stimmen beide überein, erhöht sich das Vertrauen in die Authentizität des öffentlichen Schlüssels und er kann verwendet werden. Stimmen sie nicht überein, sollte der Schlüssel auf keinen Fall verwendet werden. Wir werden in Abschnitt 50.1.7 noch einmal auf diese Problematik zurückkommen.
Zufallszahlen wurden bereits in Abschnitt 17.1 vorgestellt. In kryptografischen Anwendungen werden allerdings bessere Zufallszahlengeneratoren benötigt, als in den meisten Programmiersprachen implementiert sind. Einerseits sollte die Verteilung der Zufallszahlen besser sein, andererseits wird eine größere Periodizität gefordert (das ist die Länge der Zahlensequenz, nach der sich eine Folge von Zufallszahlen frühestens wiederholt). Zudem muss die nächste Zahl der Folge praktisch unvorhersagbar sein - selbst wenn deren Vorgänger bekannt sind.
 |
Es ist bekannt, dass sich mit deterministischen Maschinen (wie Computerprogramme es beispielsweise sind) keine echten Zufallszahlen erzeugen lassen. Eigentlich müssten wir daher von Pseudo-Zufallszahlen sprechen, um darauf hinzuweisen, dass unsere Zufallszahlengeneratoren stets deterministische Zahlenfolgen erzeugen. Mit der zusätzlichen Forderung kryptografischer Zufallszahlen, praktisch unvorhersagbare Zahlenfolgen zu generieren, wird diese Unterscheidung an dieser Stelle unbedeutend. Tatsächlich besteht der wichtigste Unterschied zu »echten« Zufallsgeneratoren nur noch darin, dass deren Folgen nicht zuverlässig reproduziert werden können (was bei unseren Pseudo-Zufallszahlen sehr wohl der Fall ist). Wir werden im Folgenden daher den Begriff »Zufallszahl« auch dann verwenden, wenn eigentlich »Pseudo-Zufallszahl« gemeint ist. |
|
 |
Die Klasse SecureRandom des Pakets java.security implementiert einen Generator für kryptografische Zufallszahlen, der die oben genannten Eigenschaften besitzt. Er wird durch Aufruf der Methode getInstance ähnlich instanziert wie ein Message Digest:
public static SecureRandom getInstance(String algorithm) throws NoSuchAlgorithmException |
java.security.MessageDigest |
Als Algorithmus ist beispielsweise »SHA1PRNG« im JDK 1.2 implementiert. Hierbei entstehen die Zufallszahlen aus der Berechnung eines Message Digest für eine Pseudonachricht, die aus einer Kombination aus Initialwert und fortlaufendem Zähler besteht. Die Klasse SecureRandom stellt weiterhin die Methoden setSeed und nextBytes zur Verfügung:
public void setSeed(long seed) public void nextBytes(byte[] bytes) |
java.security.MessageDigest |
Mit setSeed wird der Zufallszahlengenerator initialisiert. Die Methode sollte nach der Konstruktion einmal aufgerufen werden, um den Initialwert festzulegen (andernfalls macht es der Generator selbst). Gleiche Initialwerte führen auch zu gleichen Folgen von Zufallszahlen. Mit nextBytes wird eine beliebig lange Folge von Zufallszahlen erzeugt und in dem als Argument übergebenen Byte-Array zurückgegeben.
Das folgende Listing instanziert einen Zufallszahlengenerator und erzeugt zehn Folgen zu je acht Bytes Zufallszahlen, die dann auf dem Bildschirm ausgegeben werden:
001 /* Listing5004.java */
002
003 import java.security.*;
004
005 public class Listing5004
006 {
007 /**
008 * Konvertiert ein Byte in einen Hex-String.
009 */
010 public static String toHexString(byte b)
011 {
012 int value = (b & 0x7F) + (b < 0 ? 128 : 0);
013 String ret = (value < 16 ? "0" : "");
014 ret += Integer.toHexString(value).toUpperCase();
015 return ret;
016 }
017
018 public static void main(String[] args)
019 {
020 try {
021 //Zufallszahlengenerator erstellen
022 SecureRandom rand = SecureRandom.getInstance("SHA1PRNG");
023 byte[] data = new byte[8];
024 //Startwert initialisieren
025 rand.setSeed(0x123456789ABCDEF0L);
026 for (int i = 0; i < 10; ++i) {
027 //Zufallszahlen berechnen
028 rand.nextBytes(data);
029 //Ausgeben
030 for (int j = 0; j < 8; ++j) {
031 System.out.print(toHexString(data[j]) + " ");
032 }
033 System.out.println();
034 }
035 } catch (Exception e) {
036 System.err.println(e.toString());
037 System.exit(1);
038 }
039 }
040 }
|
Listing5004.java |
Eines der Hauptprobleme bei der Anwendung symmetrischer Verschlüsselungen ist das der Schlüsselübertragung. Eine verschlüsselte Nachricht kann nämlich nur dann sicher übertragen werden, wenn der Schlüssel auf einem sicheren Weg vom Sender zum Empfänger gelangt. Je nach räumlicher, technischer oder organisatorischer Distanz zwischen beiden Parteien kann das unter Umständen sehr schwierig sein.
Mit der Erfindung der Public-Key-Kryptosysteme wurde dieses Problem Mitte der siebziger Jahre entscheidend entschärft. Bei einem solchen System wird nicht ein einzelner Schlüssel verwendet, sondern diese treten immer paarweise auf. Einer der Schlüssel ist öffentlich und dient dazu, Nachrichten zu verschlüsseln. Der anderen Schlüssel ist privat. Er dient dazu, mit dem öffentlichen Schlüssel verschlüsselte Nachrichten zu entschlüsseln.
Das Schlüsselübertragungsproblem wird nun dadurch gelöst, dass ein potenzieller Empfänger verschlüsselter Nachrichten seinen öffentlichen Schlüssel an allgemein zugänglicher Stelle publiziert. Seinen privaten Schlüssel hält er dagegen geheim. Will ein Sender eine geheime Nachricht an den Empfänger übermitteln, verwendet er dessen allgemein bekannten öffentlichen Schlüssel und überträgt die verschlüsselte Nachricht an den Empfänger. Nur mit Hilfe seines privaten Schlüssels kann dieser nun die Nachricht entziffern.
Das Verfahren funktioniert natürlich nur, wenn der öffentliche Schlüssel nicht dazu taugt, die mit ihm verschlüsselte Nachricht zu entschlüsseln. Auch darf es nicht möglich sein, mit vertretbarem Aufwand den privaten Schlüssel aus dem öffentlichen herzuleiten. Beide Probleme sind aber gelöst und es gibt sehr leistungsfähige und sichere Verschlüsselungsverfahren, die auf dem Prinzip der Public-Key-Kryptografie beruhen. Bekannte Beispiele für solche Systeme sind RSA (benannt nach ihren Erfindern Rivest, Shamir und Adleman) und DSA (Digital Signature Architecture).
Asymmetrische Kryptosysteme haben meist den Nachteil, sehr viel langsamer zu arbeiten als symmetrische. In der Praxis kombiniert man daher beide Verfahren und kommt so zu hybriden Kryptosystemen. Um eine geheime Nachricht von A nach B zu übertragen, wird dabei in folgenden Schritten vorgegangen:
Fast alle Public-Key-Kryptosysteme arbeiten in dieser Weise als Hybridsysteme. Andernfalls würde das Ver- und Entschlüsseln bei großen Nachrichten viel zu lange dauern. Ein bekanntes Beispiel für ein solches System ist PGP (Pretty Good Privacy) von Phil Zimmermann. Es wird vorwiegend beim Versand von E-Mails verwendet und gilt als sehr sicher. Freie Implementierungen stehen für viele Plattformen zu Verfügung.
 |
Das Ver- und Entschlüsseln von Daten mit Hilfe von asymmetrischen Verfahren war bis zur Version 1.3 nicht im JDK enthalten. Zwar gab es als Erweiterung zum JDK die JCE (Java Cryptography Extension), doch diese durfte nur in den USA und Kanada verwendet werden. Mit dem JDK 1.4 wurden die JCE sowie die Java Secure Socket Extension (JSSE) und der Java Authentication and Authorization Service (JAAS) fester Bestandteil des JDK. Dennoch gibt es nach wie vor einige Einschränkungen in der Leistungsfähigkeit der einzelnen Pakete, die auf US-Exportbeschränkungen zurückzuführen sind. Details können in der Dokumentation zum JDK 1.4 oder neueren Versionen nachgelesen werden. |
|
 |
Ein großer Vorteil der Public-Key-Kryptosysteme ist es, dass sie Möglichkeiten zum Erstellen und Verifizieren von digitalen Unterschriften bieten. Eine digitale Unterschrift besitzt folgende wichtige Eigenschaften:
Beide Eigenschaften sind für den elektronischen Datenverkehr so fundamental wie die Verschlüsselung selbst. Technisch basieren sie darauf, dass die Funktionsweise eines Public-Key-Kryptosystems sich umkehren lässt. Dass es also möglich ist, Nachrichten, die mit einem privaten Schlüssel verschlüsselt wurden, mit Hilfe des korrespondierenden öffentlichen Schlüssels zu entschlüsseln.
Im Prinzip funktioniert eine digitale Unterschrift so:
Will A eine Nachricht signieren, so verschlüsselt er sie mit seinem privaten Schlüssel. Jeder, der im Besitz des öffentlichen Schlüssel von A ist, kann sie entschlüsseln. Da nur A seinen eigenen privaten Schlüssel kennt, muss die Nachricht von ihm stammen. Da es keinem Dritten möglich ist, die entschlüsselte Nachricht zu modifizieren und sie erneut mit dem privaten Schlüssel von A zu verschlüsseln, ist auch die Integrität der Nachricht sichergestellt. Den Vorgang des Überprüfens der Integrität und Authentizität bezeichnet man als Verifizieren einer digitalen Unterschrift.
In der Praxis sind die Dinge wieder einmal etwas komplizierter, denn die Langsamkeit der asymmetrischen Verfahren erfordert eine etwas aufwändigere Vorgehensweise. Statt die komplette Nachricht zu verschlüsseln, berechnet A zunächst einen Message Digest der Nachricht. Diesen verschlüsselt A mit seinem privaten Schlüssel und versendet ihn als Anhang zusammen mit der Nachricht. Ein Empfänger wird die Nachricht lesen, ihren Message Digest bilden und diesen dann mit dem (mit Hilfe des öffentlichen Schlüssels von A entschlüsselten) Original-Message-Digest vergleichen. Stimmen beide überein, ist die Signatur gültig. Die Nachricht stammt dann sicher von A und wurde nicht verändert. Stimmen sie nicht überein, wurde sie ver- oder gefälscht.
Das JDK stellt Klassen zum Erzeugen und Verifizieren digitaler Unterschriften zur Verfügung. Wir wollen uns beide Verfahren in den folgenden Abschnitten ansehen. Zuvor wird allerdings ein Schlüsselpaar benötigt, dessen Generierung im nächsten Abschnitt besprochen wird.
Um digitale Unterschriften erzeugen und verifizieren zu können, müssen Schlüsselpaare erzeugt und verwaltet werden. Seit dem JDK 1.2 wird dazu eine Schlüsseldatenbank verwendet, auf die mit Hilfe des Hilfsprogramms keytool zugegriffen werden kann. keytool kann Schlüsselpaare erzeugen, in der Datenbank speichern und zur Bearbeitung wieder herausgeben. Zudem besitzt es die Fähigkeit, Zertifikate (siehe Abschnitt 50.1.7) zu importieren und in der Datenbank zu verwalten. Die Datenbank hat standardmäßig den Namen ».keystore« und liegt im Home-Verzeichnis des angemeldeten Benutzers (bzw. im Verzeichnis \windows eines Windows-95/98-Einzelplatzsystems).
keytool ist ein kommandozeilenbasiertes Hilfsprogramm, das eine große Anzahl an Funktionen bietet. Wir wollen hier nur die für den Umgang mit digitalen Unterschriften benötigten betrachten. Eine vollständige Beschreibung findet sich in der Tool-Dokumentation des JDK.
Um ein neues Schlüsselpaar zu erzeugen, ist keytool mit dem Kommando -genkey aufzurufen. Zusätzlich müssen weitere Parameter angegeben werden:
Die Optionen für den Schlüssel- und Signaturtyp (-keyalg und -sigalg) sowie die Schlüssellänge (-keysize) und die Gültigkeitsdauer (-validity) sollen unspezifiziert bleiben (und daher gemäß den eingebauten Voreinstellungen belegt werden). Zusätzlich besitzt jede Schlüsseldatenbank ein Zugriffspasswort, das mit der Option -storepass (oder alternativ in der Eingabezeile) angegeben wird. Schließlich besitzt jeder private Schlüssel ein Schlüsselpasswort, das mit der Option -keypass (oder über die Eingabezeile) angegeben wird.
Wir wollen zunächst ein Schlüsselpaar mit dem Aliasnamen
»hjp3« erzeugen und mit dem Passwort »hjp3key«
vor unberechtigtem Zugriff schützen. Die Schlüsseldatenbank
wird beim Anlegen des ersten Schlüssels automatisch erzeugt und
bekommt das Passwort »hjp3ks« zugewiesen. Wir verwenden
dazu folgendes Kommando:
c:\-->keytool -genkey -alias hjp3 -dname
"CN=Guido Krueger,O=Computer Books,C=de"
Enter keystore password: hjp3ks
Enter key password for <hjp3>
(RETURN if same as keystore password): hjp3key
Nun wird ein DSA-Schlüsselpaar der Länge 1024 mit einer
Gültigkeitsdauer von 90 Tagen erzeugt. Zur Überprüfung
kann das Kommando -list (in
Kombination mit -v) angegeben
werden:
C:\--->keytool -alias hjp3 -list -v
Enter keystore password: hjp3ks
Alias name: hjp3
Creation date: Sun Dec 26 17:11:36 GMT+01:00 1999
Entry type: keyEntry
Certificate chain length: 1
Certificate[1]:
Owner: CN=Guido Krueger, O=Computer Books, C=de
Issuer: CN=Guido Krueger, O=Computer Books, C=de
Serial number: 38663e2d
Valid from: Sun Dec 26 17:11:25 GMT+01:00 1999 until: Sat Mar 25 17:11:25 GMT+01:00 2000
Certificate fingerprints:
MD5: D5:73:AB:06:25:16:7F:36:27:DF:CF:9D:C9:DE:AD:35
SHA1: E0:A4:39:65:60:06:48:61:82:5E:8C:47:8A:2B:04:A4:6D:43:56:05
Gleichzeitig wird ein Eigenzertifikat für den gerade generierten öffentlichen Schlüssel erstellt. Es kann dazu verwendet werden, digitale Unterschriften zu verifizieren. Jedes Zertifikat in der Schlüsseldatenbank (und damit jeder eingebettete öffentliche Schlüssel) gilt im JDK automatisch als vertrauenswürdig.
Wie erwähnt, entsteht eine digitale Unterschrift zu einer Nachricht durch das Verschlüsseln des Message Digest der Nachricht mit dem privaten Schlüssel des Unterzeichnenden. Nachdem wir nun ein Schlüsselpaar erstellt haben, können wir es dazu verwenden, beliebige Dateien zu signieren.
Dazu wird die Klasse Signature des Pakets java.security verwendet. Ihre Programmierschnittstelle ähnelt der der Klasse MessageDigest: Zunächst wird ein Objekt mit Hilfe einer Factory-Methode beschafft, dann wird es initialisiert und schließlich werden die Daten durch wiederholten Aufruf von update übergeben. Nachdem alle Daten angegeben wurden, berechnet ein letzter Methodenaufruf das Resultat.
Ein Signature-Objekt kann wahlweise zum Signieren oder zum Verifizieren verwendet werden. Welche der beiden Funktionen aktiviert wird, ist nach der Instanzierung durch den Aufruf einer Initialisierungsmethode festzulegen. Ein Aufruf von initSign initialisiert das Objekt zum Signieren, ein Aufruf von initVerify zum Verifizieren.
public static Signature getInstance(String algorithm) throws NoSuchAlgorithmException public final void initSign(PrivateKey privateKey) throws InvalidKeyException public final void initVerify(PublicKey publicKey) throws InvalidKeyException |
java.security.Signature |
 |
Als Argument von getInstance wird der gewünschte Signier-Algorithmus übergeben. Auch hier wird - wie an vielen Stellen im Security-API des JDK - eine Strategie verfolgt, nach der die verfügbaren Algorithmen konfigurier- und austauschbar sind. Dazu wurde ein Provider-Konzept entwickelt, mit dessen Hilfe dem API Klassenpakete zur Verfügung gestellt werden können, die Funktionalitäten des Security-Pakets teilweise oder ganz austauschen. Falls der Provider beim Aufruf von getInstance nicht angegeben wird, benutzt die Methode den Standard-Provider »SUN«, der zusammen mit dem JDK ausgeliefert wird. Der zu dem von uns generierten Schlüssel passende Algorithmus ist »SHA/DSA«. |
|
 |
Die zum Aufruf der init-Methoden benötigten Schlüssel können aus der Schlüsseldatenbank beschafft werden. Auf sie kann mit Hilfe der Klasse KeyStore des Pakets java.security zugegriffen werden. Dazu wird zunächst ein KeyStore-Objekt instanziert und durch Aufruf von load mit den Daten aus der Schlüsseldatenbank gefüllt. Mit getKey kann auf einen privaten Schlüssel zugegriffen werden, mit getCertificate auf einen öffentlichen:
public static KeyStore getInstance(String type)
throws KeyStoreException
public final Key getKey(String alias, char[] password)
throws KeyStoreException,
NoSuchAlgorithmException,
UnrecoverableKeyException
public final Certificate getCertificate(String alias)
throws KeyStoreException
|
java.security.KeyStore |
 |
 |
Das von getCertificate zurückgegebene Objekt vom Typ Certificate stammt nicht aus dem Paket java.security, sondern java.security.cert. Das in java.security vorhandene gleichnamige Interface wurde bis zum JDK 1.1 verwendet, ab 1.2 aber als deprecated markiert. Wenn nicht mit qualifizierten Klassennamen gearbeitet wird, muss daher die import-Anweisung für java.security.cert.Certificate im Quelltext vor der import-Anweisung von java.security.Certificate stehen. |
|
 |
Die Klasse Certificate besitzt eine Methode getPublicKey, mit der auf den im Zertifikat enthaltenen öffentlichen Schlüssel zugegriffen werden kann:
public PublicKey getPublicKey() |
java.security.cert.Certificate |
Ist das Signature-Objekt initialisiert, wird es durch Aufruf von update mit Daten versorgt. Nachdem alle Daten übergeben wurden, kann mit sign die Signatur abgefragt werden. Wurde das Objekt zum Verifizieren initialisiert, kann das Ergebnis durch Aufruf von verify abgefragt werden:
public final byte[] sign() throws SignatureException public final boolean verify(byte[] signature) throws SignatureException |
java.security.Signature |
Nach diesen Vorüberlegungen können wir uns nun das Programm zum Erstellen einer digitalen Unterschrift ansehen. Es erwartet zwei Kommandozeilenargumente: den Namen der zu signierenden Datei und den Namen der Datei, in die die digitale Unterschrift ausgegeben werden soll.
001 /* DigitalSignature.java */
002
003 import java.io.*;
004 import java.security.cert.Certificate;
005 import java.security.*;
006
007 public class DigitalSignature
008 {
009 static final String KEYSTORE = "c:\\windows\\.keystore";
010 static final char[] KSPASS = {'h','j','p','3','k','s'};
011 static final String ALIAS = "hjp3";
012 static final char[] KEYPASS = {'h','j','p','3','k','e','y'};
013
014 public static void main(String[] args)
015 {
016 try {
017 //Laden der Schlüsseldatenbank
018 KeyStore ks = KeyStore.getInstance("JKS");
019 FileInputStream ksin = new FileInputStream(KEYSTORE);
020 ks.load(ksin, KSPASS);
021 ksin.close();
022 //Privaten Schlüssel "hjp3" lesen
023 Key key = ks.getKey(ALIAS, KEYPASS);
024 //Signatur-Objekt erstellen
025 Signature signature = Signature.getInstance("SHA/DSA");
026 signature.initSign((PrivateKey)key);
027 //Eingabedatei einlesen
028 FileInputStream in = new FileInputStream(args[0]);
029 int len;
030 byte[] data = new byte[1024];
031 while ((len = in.read(data)) > 0) {
032 //Signatur updaten
033 signature.update(data, 0, len);
034 }
035 in.close();
036 //Signatur berechnen
037 byte[] result = signature.sign();
038 //Signatur ausgeben
039 FileOutputStream out = new FileOutputStream(args[1]);
040 out.write(result, 0, result.length);
041 out.close();
042 } catch (Exception e) {
043 System.err.println(e.toString());
044 System.exit(1);
045 }
046 }
047 }
|
DigitalSignature.java |
Will beispielsweise der Benutzer, dessen privater Schlüssel unter
dem Aliasnamen »hjp3« in der Schlüsseldatenbank gespeichert
wurde, die Datei DigitalSignature.java
signieren und das Ergebnis in der Datei ds1.sign
abspeichern, so ist das Programm wie folgt aufzurufen:
C:\--->java DigitalSignature DigitalSignature.java ds1.sign
Das Programm zum Verifizieren arbeitet ähnlich wie das vorige. Statt mit initSign wird das Signature-Objekt nun mit initVerify initialisiert und das Ergebnis wird nicht durch Aufruf von sign, sondern durch Aufruf von verify ermittelt.
001 /* VerifySignature.java */
002
003 import java.io.*;
004 import java.security.cert.Certificate;
005 import java.security.*;
006
007 public class VerifySignature
008 {
009 static final String KEYSTORE = "c:\\windows\\.keystore";
010 static final char[] KSPASS = {'h','j','p','3','k','s'};
011 static final String ALIAS = "hjp3";
012
013 public static void main(String[] args)
014 {
015 try {
016 //Laden der Schlüsseldatenbank
017 KeyStore ks = KeyStore.getInstance("JKS");
018 FileInputStream ksin = new FileInputStream(KEYSTORE);
019 ks.load(ksin, KSPASS);
020 ksin.close();
021 //Zertifikat "hjp3" lesen
022 Certificate cert = ks.getCertificate(ALIAS);
023 //Signature-Objekt erstellen
024 Signature signature = Signature.getInstance("SHA/DSA");
025 signature.initVerify(cert.getPublicKey());
026 //Eingabedatei lesen
027 FileInputStream in = new FileInputStream(args[0]);
028 int len;
029 byte[] data = new byte[1024];
030 while ((len = in.read(data)) > 0) {
031 //Signatur updaten
032 signature.update(data, 0, len);
033 }
034 in.close();
035 //Signaturdatei einlesen
036 in = new FileInputStream(args[1]);
037 len = in.read(data);
038 in.close();
039 byte[] sign = new byte[len];
040 System.arraycopy(data, 0, sign, 0, len);
041 //Signatur ausgeben
042 boolean result = signature.verify(sign);
043 System.out.println("verification result: " + result);
044 } catch (Exception e) {
045 System.err.println(e.toString());
046 System.exit(1);
047 }
048 }
049 }
|
VerifySignature.java |
Soll die Datei DigitalSignature.java
mit der im vorigen Beispiel erstellten Signatur verifiziert werden,
kann das durch folgendes Kommando geschehen:
C:\--->java VerifySignature DigitalSignature.java ds1.sign
verification result: true
Wird nur ein einziges Byte in DigitalSignature.java verändert, ist die Verifikation negativ und das Programm gibt false aus. Durch eine erfolgreich verifizierte digitale Unterschrift können wir sicher sein, dass die Datei nicht verändert wurde. Zudem können wir sicher sein, dass sie mit dem privaten Schlüssel von »hjp3« signiert wurde, denn wir haben sie mit dessen öffentlichen Schlüssel verifiziert.
Ein großes Problem bei der Public-Key-Kryptografie besteht darin, die Authentizität von öffentlichen Schlüsseln sicherzustellen. Würde beispielsweise B einen öffentlichen Schlüssel publizieren, der glaubhaft vorgibt, A zu gehören, könnte dies zu verschiedenen Unannehmlichkeiten führen:
Einen Schutz gegen derartigen Missbrauch bieten Zertifikate. Ein Zertifikat ist eine Art Echtheitsbeweis für einen öffentlichen Schlüssel und erfüllt damit ähnliche Aufgaben wie ein Personalausweis oder Reisepass. Ein Zertifikat besteht meist aus folgenden Teilen:
Die Glaubwürdigkeit des Zertifikats hängt von der Glaubwürdigkeit des Ausstellers ab. Wird dieser als vertrauenswürdig angesehen, d.h., kann man seiner digitialen Unterschrift trauen, so wird man auch dem Zertifikat trauen und den darin enthaltenen öffentlichen Schlüssel akzeptieren.
Dieses Vertrauen kann einerseits darauf basieren, dass der Aussteller eine anerkannte Zertifizierungsautorität ist (auch Certification Authority, kurz CA, genannt), deren öffentlicher Schlüssel bekannt und deren Seriösität institutionell manifestiert ist. Mit anderen Worten: dessen eigenes Zertifikat in der eigenen Schlüsselverwaltung bekannt und als vertrauenswürdig deklariert ist. Andererseits kann das Vertrauen in das Zertifikat daher stammen, dass der Aussteller persönlich bekannt ist, sein öffentlicher Schlüssel eindeutig nachgewiesen ist und seiner Unterschrift Glauben geschenkt wird.
Der erste Ansatz wird beispielsweise bei X.509-Zertifikaten verfolgt. Institute, die derartige Zertifikate ausstellen, werden meist staatlich autorisiert und geprüft. Beispiele dafür sind VeriSign, Thawte oder das TA Trustcenter. Der zweite Ansatz liegt beispielsweise den Zertifikaten in PGP zugrunde. Hier ist es sogar möglich, öffentliche Schlüssel mit mehreren digitalen Unterschriften unterschiedlicher Personen zu signieren und so die Glaubwürdigkeit (bzw. ihre Reichweite) zu erhöhen.
Zertifizierungsinstitute stellen meist auch Schlüsseldatenbanken zur Verfügung, aus denen Zertifikate abgerufen werden können. Diese dienen auch als Anlaufstelle, um ungültig gewordene oder unbrauchbare Zertifikate zu registrieren. Lokale Schlüsselverwaltungen können sich mit diesen Informationen synchronisieren, um ihren eigenen Schlüsselbestand up-to-date zu halten.
| Titel | Inhalt | Suchen | Index | DOC | Handbuch der Java-Programmierung, 7. Auflage, Addison Wesley, Version 7.0 |
| << | < | > | >> | API | © 1998, 2011 Guido Krüger & Heiko Hansen, http://www.javabuch.de |